0139
Calibrationless Parallel Imaging in Multi Echo/Contrast Data1Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 2National Nanotechnology Center, Pathum Thani, Thailand
Synopsis
Parallel imaging relies on fully-sampled calibration data to estimate k-space kernels or sensitivities used to reconstruct subsampled acquisitions. Emerging techniques use low-rank modeling, or joint estimation of sensitivities and image content via nonlinear optimization, to reduce the dependency on calibration data. In a typical study, images at multiple echoes/contrasts are acquired using the same coil sensitivities. Here, we exploit this joint information to dramatically improve conditioning of
Introduction
Conventional parallel imaging requires an auto-calibration signal (ACS) to estimate sensitivities or k-space kernels for reconstruction, which increases the overall scan time. Inconsistency due to motion or physiological noise in the calibration may lead to significant artifacts in the reconstructed images (1). Moreover, in dynamic, spectroscopic and non-Cartesian imaging, acquiring sufficient calibration data can be challenging or not possible at all. Emerging techniques either use low-rank modeling (2-4), or jointly estimate sensitivities and images (5,6) to reduce the dependence on calibration.
In this work, we jointly reconstruct sensitivities and image content by extending the nonlinear inversion reconstruction approach (NLINV) (6) and show that no calibration is required for multi-echo and for multi-contrast acquisitions. Our Joint-NLINV leverages the fact that coil sensitivities are shared across echoes/contrasts to dramatically reduce the number of unknowns. We also extend Total Variation (TV) (7) to permit joint regularization across images, and initialize the nonlinear optimization using a composite image. This is made possible through complementary k-space sampling since a fully sampled k-space with reduced aliasing can be obtained through summation across echoes/contrasts.
We demonstrate calibrationless reconstruction for i) multi-echo spin-echo, ii) multi-echo MPRAGE (8), iii) phase-cycled balanced SSFP, and iv) a multi-contrast protocol, and show at least 6-fold reduced RMSE from our Joint-NLINV over standard NLINV.
Matlab code and data are available at http://bit.ly/2eovLRC
Theory
We jointly solve for images and sensitivities so that they match the acquired data :
where is the sampling pattern for image , is the Fourier transform and is the k-space data belonging to coil of image . This signal equation can be cast as, , where is a nonlinear operator acting on the unknowns . The nonlinear operation can be linearized around an initial guess using the Jacobian ,
which is then solved for the update . We constrain the sensitivities to be smooth via Sobolev norm (6), and jointly regularize the multiple images through norm,
Here penalizes high frequencies in sensitivities, and is the spatial gradient operator. Optimization for is performed with nonlinear conjugate gradient (9), and are reduced gradually by 2-fold after each outer Gauss-Newton iteration to avoid over-regularizing.
Acquisition
Four fully-sampled datasets were retrospectively undersampled:
i) Multi-echo spin-echo: using parameters from (10), TE1=∆TE=11.5ms, 8 echoes, FOV=240×180mm2, mtx=256×208, and slice thickness=3mm, 12-channel reception.
ii) ME-MPRAGE: TE1=1.7ms, ∆TE=1.9ms, 4 echoes, 1mm isotropic, mtx=256×240×192, BW=651Hz/pixel, 32-channel reception.
iii) Phase-cycled bSSFP: TR/TE=3.37/1.57ms at FOV=240×240mm2, mtx=160×160, slice thickness=4.5mm, BW=845Hz/pixel, and 32-channel reception. Four phase-cycles (0, π/2, π, 3π/2) were collected.
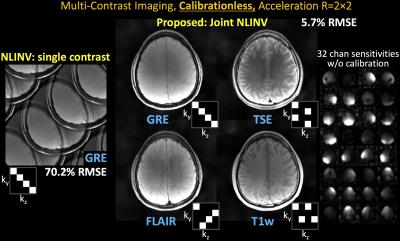
iv) T1w, FLAIR, TSE and GRE dataset: as per (11), FOV=224×224mm2, mtx=256×256, slice thickness=4mm, 32-channel reception.
Reconstruction
Data were reconstructed using NLINV and Joint-NLINV without calibration data. All experiments used R=2×2 acceleration with complementary undersampling, and initial TV parameter =0.1, Newton steps=9, CG (inner) iterations=75. For the multi-contrast data (set iv), the use of CAIPI undersampling was also explored. RMSEs were computed inside the brain mask. Specific settings were:
Datasets i&ii): starting parameter =0.001, using composite echo for initialization.
Dataset iii&iv): due to phase mismatch between bSSFP cycles and large differences in multi-contrast data, a composite image with reduced aliasing could not be formed for these datasets; hence images were initialized with a vector of ones and a higher initial regularization =0.01 and 0.1 were used respectively.
Results & Discussion
With no ACS, NLINV reconstruction is highly ill-conditioned and results in large errors (Figs1-4). With Joint-NLINV, shared coil sensitivities and joint sparsity across multiple echoes/contrasts are exploited to dramatically improve the reconstruction. In particular, proposed Joint-NLINV obviates the need for calibration in multi-echo/contrast data, with at least 6-fold reduced RMSE over standard NLINV method across all cases.
Complementary sampling permits formation of a composite image by summing the k-space across echoes. For spin-echo and MPRAGE where phase discrepancy between echoes is low, composite echo has reduced aliasing and can be used for initialization. For phase-cycled bSSFP and multi-contrast reconstruction, a composite image contains significant residual aliasing and was not used. This necessitated a larger starting parameter , which is reduced over iterations to still result in negligible level of regularization in the final reconstruction.
Conclusion
Harnessing shared sensitivity and edge structures across echoes/contrasts dramatically improve the conditioning of nonlinear inversion, allowing calibrationless parallel imaging with high quality.Acknowledgements
NIH grant numbers R01EB020613, R24MH106096, R01EB019437, P41EB015896 and R01EB017337.References
1. Polimeni JR, Bhat H, Witzel T, Benner T, Feiweier T, Inati SJ, Renvall V, Heberlein K, Wald LL. Reducing sensitivity losses due to respiration and motion in accelerated echo planar imaging by reordering the autocalibration data acquisition. Magn. Reson. Med. 2016;75:665–679. doi: 10.1002/mrm.25628.
2. Trzasko JD, Manduca A. Calibrationless parallel MRI using CLEAR. In: 2011 Conference Record of the Forty Fifth Asilomar Conference on Signals, Systems and Computers (ASILOMAR). IEEE; 2011. pp. 75–79. doi: 10.1109/ACSSC.2011.6189958.
3. Shin PJ, Larson PEZ, Ohliger MA, Elad M, Pauly JM, Vigneron DB, Lustig M. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn. Reson. Med. 2014;72:959–970. doi: 10.1002/mrm.24997.
4. Haldar JP, Zhuo J. P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data. Magn. Reson. Med. 2016;75:1499–1514. doi: 10.1002/mrm.25717.
5. Ying L, Sheng J. Joint image reconstruction and sensitivity estimation in SENSE (JSENSE). Magn. Reson. Med. 2007;57:1196–1202.
6. Uecker M, Hohage T, Block KT, Frahm J. Image reconstruction by regularized nonlinear inversion--joint estimation of coil sensitivities and image content. Magn. Reson. Med. 2008;60:674–82.
7. Knoll F, Clason C, Bredies K, Uecker M, Stollberger R. Parallel imaging with nonlinear reconstruction using variational penalties. Magn. Reson. Med. 2012;67:34–41. doi: 10.1002/mrm.22964.
8. van der Kouwe AJW, Benner T, Salat DH, Fischl B. Brain morphometry with multiecho MPRAGE. Neuroimage 2008;40:559–569. doi: 10.1016/j.neuroimage.2007.12.025.
9. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007;58:1182–95. doi: 10.1002/mrm.21391.
10. Zhao B, Lu W, Hitchens TK, Lam F, Ho C, Liang Z-P. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magn. Reson. Med. 2015;74:489–498. doi: 10.1002/mrm.25421.
11. Chatnuntawech I, Martin A, Bilgic B, Setsompop K, Adalsteinsson E, Schiavi E. Vectorial total generalized variation for accelerated multi-channel multi-contrast MRI. Magn. Reson. Imaging 2016;34:1161–1170. doi: 10.1016/j.mri.2016.05.014.
Figures
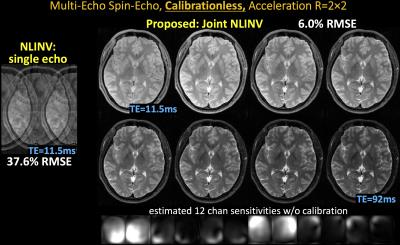
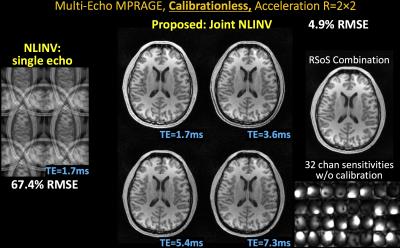
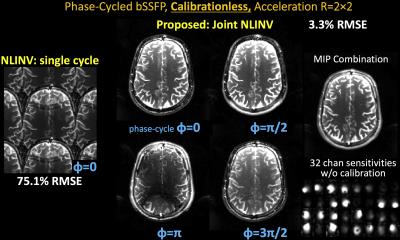
Fig3. Balanced SSFP is an efficient sequence with unique contrast, but suffers from banding artifacts due to B0 sensitivity. These artifacts can be mitigated through phase-cycling which involves multiple acquisitions at different phase offsets. Joint NLINV allows calibrations bSSFP at 4-fold acceleration with four phase-cycles, and leads to a banding free Max Intensity Projection (MIP) combination.