1250
Robust high-quality multi-shot EPI with low-rank prior and machine learning1Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 2National Nanotechnology Center, Pathum Thani, Thailand, 3Siemens Healthcare, Erlangen, Germany, 4Siemens Healthcare, Charlestown, MA, United States, 5Department of Electrical Engineering, Stanford University, Stanford, CA, United States
Synopsis
We introduce acquisition and reconstruction strategies for robust, high-quality multi-shot EPI (msEPI) without phase navigators. We extend the MUSSELS low-rank constrained parallel imaging technique to perform Virtual Coil (VC) reconstruction, and demonstrate diffusion imaging with sub-millimeter in-plane resolution using 55% partial-Fourier (PF) sampling. We propose Blip Up-Down Acquisition (BUDA) using interleaved blip-up and -down phase encoding, and incorporate B0 forward-modeling into MUSSELS to enable distortion- and navigator-free msEPI. We improve the acquisition efficiency by developing Simultaneous MultiSlice (SMS-)MUSSELS, and combine it with machine learning (ML) to provide Rtotal=16-fold acceleration with 3-shots. Deploying this in a spin-and-gradient-echo (SAGE) scan with signal modeling allows for whole-brain T2 and T2* mapping with high geometric fidelity in 12.5 seconds.
Introduction
msEPI allows high-resolution imaging with reduced distortion, but combining shots is prohibitively difficult because of shot-to-shot phase variations. Existing navigator-free approaches employ parallel imaging (PI) to reconstruct each shot, from which phase variations are estimated (1,2). This imposes a limit on the distortion reduction since PI breaks down beyond Rinplane>4 acceleration.
MUSSELS (3) is a low-rank constrained PI approach (4,5) which improves acceleration capability, but requires a large number of shots (Rinplane=8 with 4-shots). We propose SMS-MUSSELS acquisition/reconstruction to further accelerate msEPI, demonstrate its extension to VC concept (6) and obtain high-quality images from a PF=55% acquisition. We propose Blip Up-Down Acquisition (buda) where msEPI sampling is performed with interleaved blip-up and -down acquisitions, and combine these shots with B0 forward-modeling and MUSSELS to yield distortion-free images. Finally, we push the acceleration to Rtotal=16 (RinplanexSMS=8x2) and combine ML and SMS-MUSSELS to obtain 1x1x3mm3 whole-brain T2 and T2* maps from a 12.5sec acquisition.
Code/data: https://bit.ly/2qzhA1t
Virtual Coil (VC-) MUSSELS
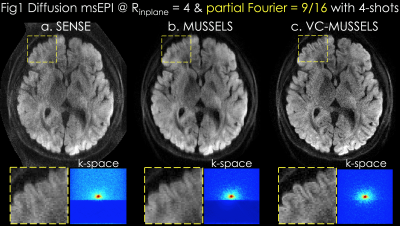
Acquisition: 0.85x0.85x3mm3 resolution diffusion data were acquired at b=1000s/mm2 using 32-channel reception at 3T with TE/TR=46/2000ms (7). 4-shots were collected at Rinplane=4 and PF=55%.
Reconstruction: In Fig1a, SENSE (8) was performed for each shot separately, followed by magnitude averaging over the 4-shots. MUSSELS in Fig1b was obtained via
where is the undersampled Fourier operator in shot , are ESPIRiT sensitivities (9), and are the shot k-space data. enforces low-rank prior on the block-Hankel representation of the multi-shot data , which is formed by concatenating the images from shots. Proposed VC-MUSSELS (Fig1c) incorporates conjugate shot-images into the low-rank constraint, whereby conjugate-symmetric k-space helps estimate the missing data and improves the resolution (yellow boxes).
Blip Up-Down Acquisition (buda-) MUSSELS
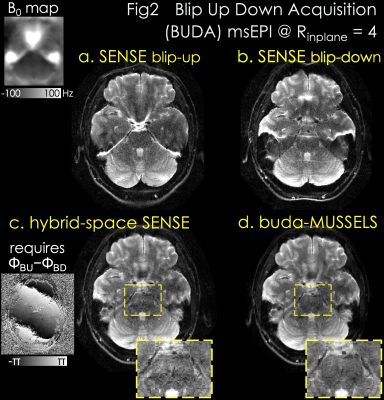
Acquisition: 1x1x5mm3 spin-echo EPI at Rinplane=4 was acquired with TE/TR=75/3000ms, and two shots with blip-up and -down polarity were collected.
Reconstruction: Fig2a&b demonstrate separate SENSE for blip-up and -down acquisitions with significant distortion. Hybrid-space SENSE (10) jointly reconstructs the 2-shots by using their phase difference and B0 information from topup (9,10) (Fig2c). buda-MUSSELS obviates the need for phase estimation, and eliminates distortion by incorporating the fieldmap in PI to improve image quality and SNR (Fig2d, yellow boxes).
Network Estimated Artifacts for Tampered Reconstruction (NEATR) combines SMS-MUSSELS with ML
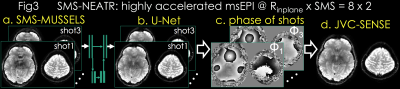
SMS-MUSSELS: is developed to combine MUSSELS with SMS using the readout-extended FOV concept (13). This represents SMS as undersampling in the kx-axis by concatenating the two slices along the readout (Fig3a). In-plane and slice acceleration could thus be captured using with kx-ky undersampling and push the acceleration to RinplanexSMS=8x2 for spin-and-gradient echo (SAGE (14)) msEPI.
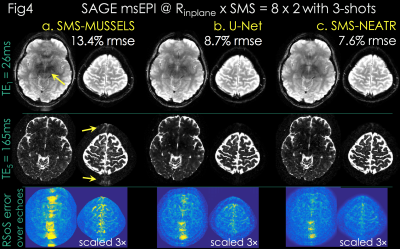
Due to high acceleration, SMS-MUSSELS failed to provide clean images using 3-shots (Rnet=16/3, Fig3a&4a). A network with U-Net architecture (15) was utilized to mitigate the SMS-MUSSELS artifacts. To provide “fully-sampled” data to train the network, four volunteers were scanned with 8-shots at prospective Rinplane=8 (FOV=224x224x120mm3, 1x1x3mm3 resolution, TEs=26/61/61/130/165ms, TR=8.3sec). MUSSELS reconstruction of this Rnet=1 data yielded references images.
Residual U-Net (Fig3b): learned a mapping between the 3-shot SMS-MUSSELS and the error relative to the reference images. Three volunteers’ data were used for training and the fourth subject was reserved for testing. U-Net with 5 levels, -loss, leaky-ReLU activation (16) and 64 filters at the highest level was trained on 64x64 patches. Real and imaginary parts of 3-shots were presented as channels for complex-valued processing.
Joint Virtual Coil (JVC-)SENSE: The refined U-Net magnitude allows us to solve for the phase of shot with wavelet () regularization (17) (Fig3c):
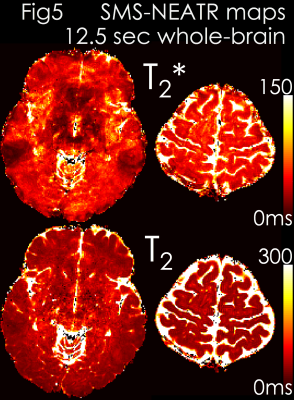
Results: Fig4 shows 2 echoes (out of 5) from a slice group where SMS-MUSSELS yielded 13.4% Rmse with ghosting/aliasing artifacts (arrows). U-Net mitigated these (8.7% error), allowing JVC-SENSE to provide clean images (7.6% Rmse). Using the SAGE signal equation yielded T2 and T2* maps with whole-brain coverage in 12.5 sec (Fig5).
Conclusion
We incorporated VC, buda and SMS concepts into MUSSELS to push the limits of PF, in-plane and slice acceleration in msEPI, and enabled high in-plane resolution, rapid structural imaging with improved geometric fidelity. SMS-NEATR took advantage of ML for accurate estimates of shot-to-shot phase variations and provided 1.8x Rmse reduction over SMS-MUSSELS. This paves the way for full synergistic combination of ML and model-based reconstruction, where deep learning could provide rapid estimates of B0 inhomogeneity to be included in buda-NEATR, and eliminate distortion without the need for topup processing.Acknowledgements
This work was supported in part by NIH research grants: R01EB020613, R01EB019437, R24MH106096, P41EB015896, and the shared instrumentation grants: S10RR023401, S10RR019307, S10RR019254, S10RR023043.References
1. Chen NK, Guidon A, Chang HC, Song AW. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). Neuroimage 2013;72:41–47. doi:
10.1016/J.NEUROIMAGE.2013.01.038.
2. Zhang Z, Huang F, Ma X, Xie S, Guo H. Self-feeding MUSE: A robust method for high resolution diffusion imaging using interleaved EPI. Neuroimage 2015;105:552–560. doi: 10.1016/J.NEUROIMAGE.2014.10.022.
3. Mani M, Jacob M, Kelley D, Magnotta V. Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magn. Reson. Med. 2017;78:494–507. doi: 10.1002/mrm.26382.
4. Haldar JP, Zhuo J. P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data. Magn. Reson. Med. 2016;75:1499–1514. doi: 10.1002/mrm.25717
5. Lobos RA, Kim TH, Hoge WS, Haldar JP. Navigator-Free EPI Ghost Correction With Structured Low-Rank Matrix Models: New Theory and Methods. IEEE Trans. Med. Imaging 2018;37:2390–2402. doi: 10.1109/TMI.2018.2822053.
6. Blaimer M, Gutberlet M, Kellman P, Breuer F, Kostler H, Griswold MA. Virtual coil concept for improved parallel MRI employing conjugate symmetric signals. Magn. Reson. Med. 2009;61:93–102.
7. Hu Y, Levine EG, Tian Q, Moran CJ, Wang X, Taviani V, Vasanawala SS, McNab JA, Daniel BA, Hargreaves BL. Motion-robust reconstruction of multishot diffusion-weighted images without phase estimation through locally low-rank regularization. Magn. Reson. Med. 2018. doi: 10.1002/mrm.27488.
8. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn. Reson. Med. 1999;42:952–962.
9. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 2014;71:990–1001. doi: 10.1002/mrm.24751.
10. Zahneisen B, Aksoy M, Maclaren J, Wuerslin C, Bammer R. Extended hybrid-space SENSE for EPI: Off-resonance and eddy current corrected joint interleaved blip-up/down reconstruction. Neuroimage 2017;153:97–108. doi: 10.1016/J.NEUROIMAGE.2017.03.052.
11. Andersson JLR, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage 2003;20:870–888. doi: 10.1016/S1053-8119(03)00336-7.
12. Smith SM, Jenkinson M, Woolrich MW, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 2004;23:S208–S219. doi: 10.1016/j.neuroimage.2004.07.051.
13. Koopmans PJ, Poser BA, Breuer FA. 2D-SENSE-GRAPPA for Fast, Ghosting-Robust Reconstruction of In-Plane and Slice Accelerated Blipped-CAIPI-EPI. In: International Society for Magnetic Resonance in Medicine 23rd Scientific Meeting, Toronto, Canada. ; 2015. p. 2410.
14. Schmiedeskamp H, Straka M, Newbould RD, Zaharchuk G, Andre JB, Olivot J-M, Moseley ME, Albers GW, Bammer R. Combined spin- and gradient-echo perfusion-weighted imaging. Magn. Reson. Med. 2012;68:30–40. doi: 10.1002/mrm.23195.
15. Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In: Medical image computing and computer-assisted intervention : MICCAI. Springer, Cham; 2015. pp. 234–241. doi: 10.1007/978-3-319-24574-4_28.
16. Maas AL, Hannun AY, Ng AY. Rectifier nonlinearities improve neural network acoustic models. ICML Work. Deep Learn. AUDIO, SPEECH Lang. Process. 2013;30:3.
17. Ong F, Cheng JY, Lustig M. General phase regularized reconstruction using phase cycling. Magn. Reson. Med. 2018;80:112–125. doi: 10.1002/mrm.27011.
Figures